Montessori Wooden Stamp Game

Stamp Game

How to use the stamp Game Materials

Introduction

• Invite the child to come and work with you.
• Show the child the material and have him first bring over the paper needed. Then show the child the material and have him bring over the box of wooden tiles as well as the tray from Introduction to Quantity.
• Show the child the 1 green tile and show the 1 unit to the child. Tell the child that it is the same as the unit bead.
• Show the child the blue tile and have him read the ‘10’ written on it. Tell the child that this is just like the ten-bar.
• Repeat for the tiles of 100 and 1000.
• Do a Three Period Lesson with the 1, 10, 100, and 1000 tiles.
• Show the child that when we take out the 1 tiles, we place them directly in front of the compartment where the other 1’s are.
• Tell the child that you are going to take out 5. Take out 5 of the 1 tiles and place them all in front of the 1 compartment.
• Put them back and give the child a few numbers to take out. Such as make 3 tens, or 5 hundreds, or 2 thousands.
• Then give the child a larger number.
• Say, “Now we are going to make a larger number. This number will have 3 units, 5 tens, 2 hundreds, 1 thousand.
• As you give the child each number, have him take out the appropriate tiles.
• Count to check the final product and then have the child put the tiles back into their compartments.

Presentation 1: Addition

To be done directly following the Introduction.

Static Addition

1. Show the child the paper on which we write our problems.
2. Tell the child that the first column is where we write the units. The second column is where we write the tens, the third column is where we write the hundreds, and the fourth column is where we write the thousands.
3. Write a number, such as 1524 and read it with the child as: 4 units, 2 tens, 5 hundreds, and 1 thousand. Then read it: 1524.
4. Have the child create the number using the tiles.
5. Tell the child that we are going to make another number.
6. Show the child that you will write this new number below the first number on the piece of paper.
7. Write: 1241 and read it with the child as before.
8. Show the child that we will place the tiles for this number a little below the other tiles.
9. Have the child create this number using the tiles.

 

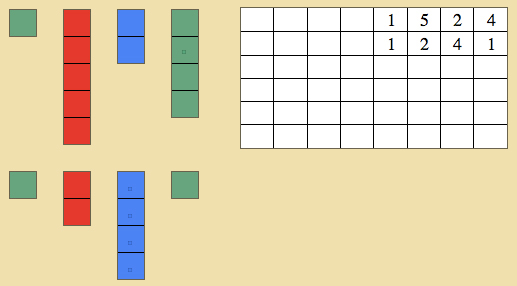
1. Tell him that we will see how much we have all together.
2. Tell the child that we show this by using the addition sign. Show the child the sign and where to place it on the paper.
3. Then draw a line under the last number using the ruler.
4. Have the child count all of the units: 4 + 1 = 5
5. Write in 5 under the units on the paper.
6. Have the child count the tens, hundreds, and thousands, each time writing the answer down.
7. Read the final answer with the child: When we have 1524 and we add 1241 we get 2765!
   
   
   
   
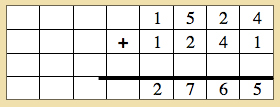
8. Allow the child a turn with another example. Guide him with questions.
   
   

Dynamic Addition

1. Have the child construct and write the first add-in, first the units, tens, hundreds, and then thousands.
2. Have the child write another add in, but guide the child so that there will be a need to change the numbers.
3. Have the child construct the two numbers using the tiles.
4. Count all of the tiles and notice that you are going to need to change some of the tiles. Have the child do so.

 

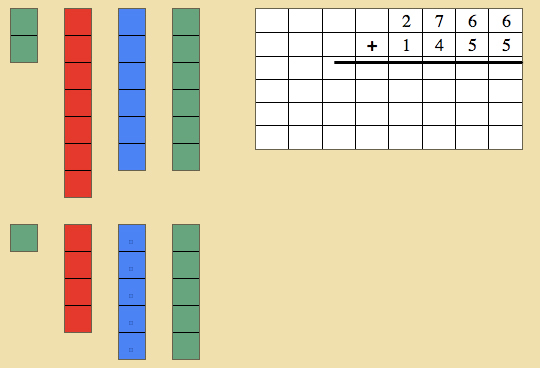
1. Read the finished problem with the child.
   
   
   
   
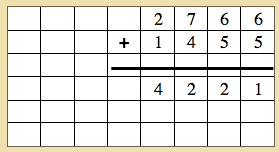
2. Allow the child a turn with another example. Guide him with questions.

Exercice

The child works alone, creating his own problems. 

Presentation 2: Substraction

Static Substraction

1. Invite the child to come and work with you.
2. Write a first number and a second number. Introduce the new subtraction sign.

 

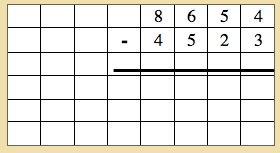
1. Have the child construct the first number.
   
   
   
   
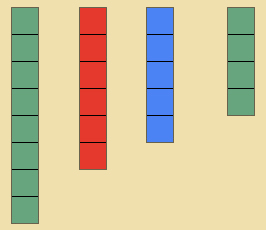
2. Tell the child that we are going to take 3 units from the four units constructed.
3. Have the child move 3 units off to the left side of the table.
4. Count how many units you have left and write the answer.
5. Have the child take 2 tens away from the 5 and more them off to the side of the table. Count and then write how many tens are left.
6. Repeat for the hundreds and thousands.
7. Read the answer with the child.

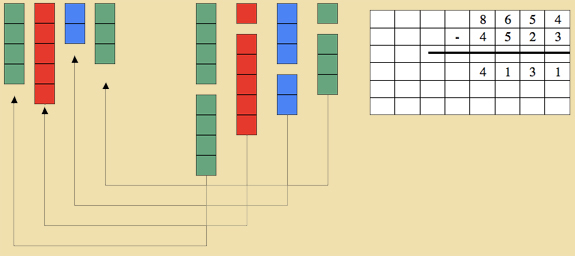
Dynamic Substraction

1. Write a first large number and a second number under it. Make sure that this will lead to dynamic subtraction.

 

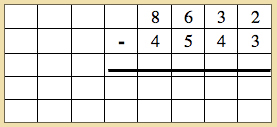
1. Have the child create the first number.
2. Ask the child how many units are we going to take away: 3 units. But as the child becomes stuck, say that we are going to have to change one of the tens for units. Take out ten units and replace it with one of the ten tiles.
3. Then have the child take 3 units away from the now 12 units. Place the unneeded tiles off to the side of the table.

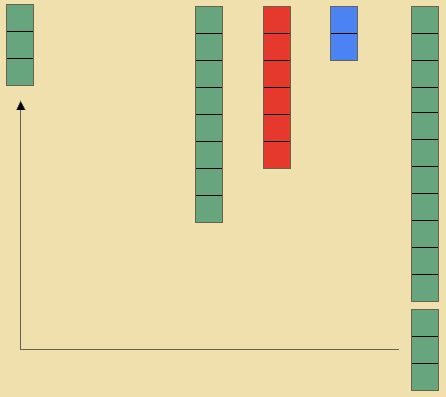
1. Have the child write how many units he has left.
2. Repeat for the tens, hundreds, and thousands. Change when needed.
3. Read the final problem with the answer with the child.
   
   
   
   
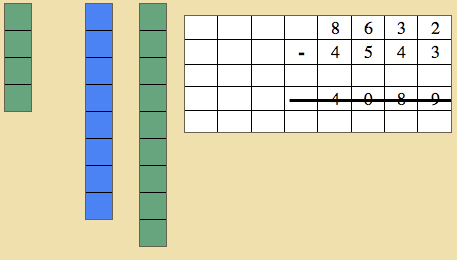
4. Repeat until the child feels comfortable to work alone. 
   
   

Exercice

The child works alone, creating his own problems. 

Presentation 3: Multiplication

Static Multiplication

1. Invite the child to come and work with you.
2. Create a problem.

 

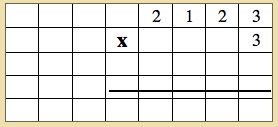
1. Introduce the new multiplication symbol to the child. “This is a new symbol for multiplication. It is called the ‘times’ symbol.
2. Read the problem with the child: 2123 times 3.
3. Have the child create 2123.
4. Read with the child and say, “Yes, this is 2123. But we want 2123 three times. Lets see you make this number a total of three times!”
5. Have the child create 2123 three times.

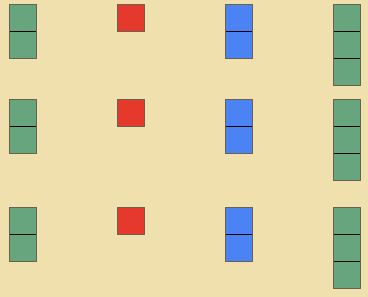
1. Slide all of the tiles from the same category up together to create only four rows.
2. Have the child count all the units and then fill in the answer on the paper.
3. Repeat for the tens, hundreds, and thousands. 
   
   
   
   

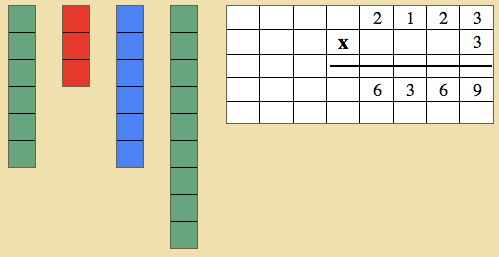
Dynamic Multiplication

1. Invite a child to come and work with you.
2. Create a problem

 

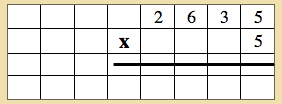
1. Read it: 2635 times 5. Make mention that we are going to take this number 5 times!
2. Take out the skittles and place them in a vertical line with ample space between them.
3. Have the child create 2635 to line up with the first skittle.
4. Have the child create 2635 four more times.
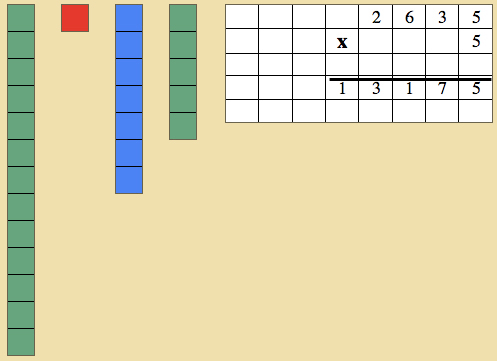
5. Have the child count the total amount of units, changing when needed.
6. Count the total amount of tens, changing when needed.
7. Count the total amount of hundreds, changing when needed.
8. Once done, have the child count what is left and write the answer on the piece of paper.

Exercice

The child works alone as shown in the presentation

Note

Although there is a limitation in the material, the child may multiply any number he may wish.

Presentation 3: Division

Static Division

1. Invite a child to come and work with you and have him bring the material to the table.
2. Create a problem.

 

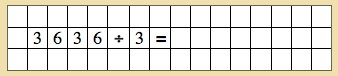
1. Introduce the two new symbols to the child.
2. Have the child create 3636 using the tiles.
3. Show the child the green skittle and place them in a row to the right of the tiles. Explain to the child that we are going to give each skittle the same amount of tiles.
4. Tell the child that when we divide, we always start with the thousands.
5. “Give” each skittle a thousand tile.
6. Notice that there are no more 1000 tiles to give.
7. “Give” each skittle a 100 tile. Notice that there are more 100 tiles. Give each skittle another 100 tile.

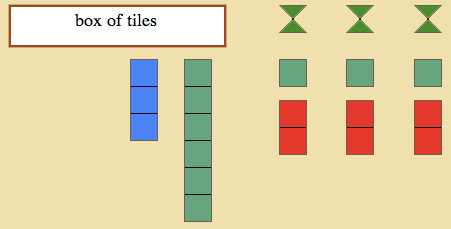
1. Give each skittle a 10 tile and notice that there are no more left to give.
2. Give each skittle a 1 tile until there are none left.
3. Tell the child: “In division, we always look at what one get, so lets see how many one skittle got.”
4. Count what one skittle got, writing in the units, the tens, the hundreds, and then the thousands.
   
   

 

Dynamic Division: no remainder

1. Invite a child to come and work with you and have him>bring the material to the table.
2. Create a problem: 6525 ¸ 5 =
3. Have the child create 6525 using the tiles.
4. remind the child that when we divide, we start with the thousand.
5. “Give” each skittle a thousand tile.
6. Notice that we have 1 left over. Change it for ten hundred tiles.
7. “Give” each skittle a hundred until there are no more hundred tiles. Notice that there are none left after we gave each skittle 3 hundreds.
8. Notice that there are not enough ten tiles to give to each skittle. Change one ten tile into 10 unit tiles and then change the second ten tile into 10 unit tiles.
9. Give each skittle a unit tile until there are none left.
10. Count how many tiles one skittle has and write down the number each number at a time.
    
    

Dynamic Division: remainder

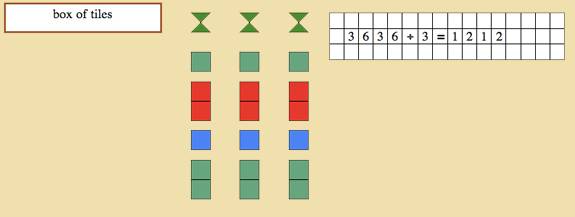
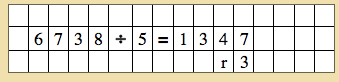
1. Create a problem for the child: 6738 ¸ 5 =
2. The procedure for this exercise is the same as in the above procedure for Division with no remainder except for the end.
3. Notice with the child that there are some unit tiles left and not enough to give to each skittle. Tell the child that these tiles are called a “remainder”. Show the child how to write the remainder. 
   
   

 

Dynamic Division: 2 level divisor

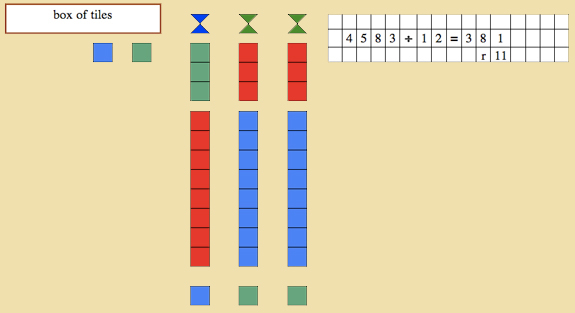
1. Invite a child to come and work with you and have him bring the material to the table.
2. Create a problem:

 

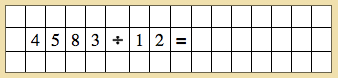
1. Have the child create 4583 using the tiles.
2. Discuss how many units there are in 12 = 2 units.
3. Place two green skittles at the top of the table.
4. Discuss how many tens there are in 12 = 1 ten.
5. Place one blue skittle at the top of the table to the left of the green skittles.
6. Begin by giving the blue skittle a tile of a thousand. Discuss with the child that if the blue skittle gets a thousand tile, the green tiles must each get a hundred tile because the green tile is ten times less than the blue tile.
7. Give each green skittle a hundred tile for every thousand tile you give to the blue skittle.
8. When there are two thousand tiles left but only a hundred tile, change one of the thousand tiles for ten hundreds. Give the last thousand to the blue skittle and two hundred tiles to the two green skittles.

1. Continue in this manner, giving the green skittles ten times less that what you give the blue skittle.
2. Once all of the tiles that can be shared are shared, remind the child that in division, we always look at what one person gets. Have the child count the tiles for one of the green skittles, writing in how many units, tens, hundreds, and thousands one skittle gets and have the child write in the remainder.

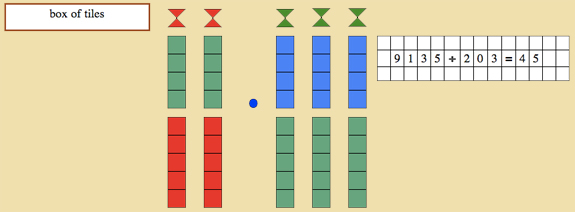
Dynamic Division: 3 level divisor

This is to be done in the same way as Division with a 2 level divisor. The hundred should be represented by a red skittle.

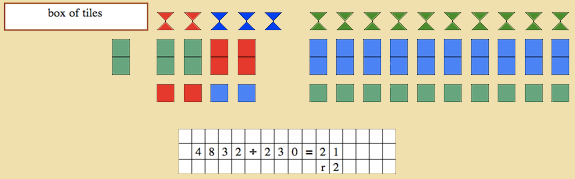
Dynamic Division: 3 level divisor with a zero in the tens

As above but since there are no tens, “keep” the place of the ten by placing a blue circle where the skittle would have gone. Tell the child that this “holds” the tens spot. From time to time, ask the child what the ten would get if it was not a zero. 

Move the circle down before beginning to give out a new grouping of tiles. (The child should answer that he would get 100 times less than the hundred skittle.) See diagram for finished product:

 

 

Dynamic Division: 3 level divisor with a zero in the units

As above but since there are no units, “keep” the place of the unit by placing a green circle where the skittle would have gone. Tell the child that this “holds” the unit’s spot. From time to time, ask the child what the unit would get if it was not a zero.

Move the circle down before beginning to give out a new grouping of tiles. (The child should answer that the unit would get 10 times less than the ten skittle.) Once the operation is complete, remind the child that in division we always look at what one gets so you will need to divide what a ten skittle got into ten unit skittles. See diagram for finished product:

 

Exercice

The child can work alone, creating his own division problems to solve as he was shown in the presentations. 

Purpose

Direct
To give the child the opportunity of carrying out individual 
Exercises in the four operations. Previously, he needed the collaboration of other children to do these operations with the bead material of the decimal system.

Long division
As above, and so become more familiar with all the steps involved in long division. The use of this more symbolic material helps the child to move closer towards abstraction. 

Control of Error
The child’s growing knowledge.

Age 
To 5 1/2 years for addition, subtraction, multiplication and short division.
To 6 years for long division.